Dave's Math Tables: Vectors
(Math | OddsEnds | Vectors)

Notation: The lower case letters a-h, l-z denote scalars.Uppercase bold A-Z denote vectors. Lowercase boldi, j, k denote unit vectors. <a, b>denotes a vector with components a and b. <x1, .., xn>denotes vector with n components of which are x1, x2, x3, ..,xn. |R| denotes the magnitude of the vector R.

|<a, b>| = magnitude of vector = 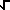sqrt(a 2+ b 2)

|<x1, .., xn>| = 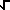sqrt(x12+ .. + xn2)

<a, b> + <c, d> = <a+c, b+d>

<x1, .., xn> + <y1, .., yn>= < x1+y1, .., xn+yn>

k <a, b> = <ka, kb>

k <x1, .., xn> = <k x1, .., k x2>

<a, b> .<c, d> = ac + bd

<x1, .., xn> .<y1, ..,yn> = x1 y1 + .. + xn yn>

R . S= |R| |S| cos theta(theta = angle betweenthem)

R . S= S . R

(a R) . (bS) = (ab) R . S

R . (S + T)= R . S+ R . T

R . R = |R| 2

|R x S| = |R| |S| sin theta(theta = angle betweenboth vectors). Direction of R x S is perpendicularto A & B and according to the right hand rule.

        | i  j  k |
R x S = | r1 r2 r3 | = / |r2 r3|   |r3 r1|   |r1 r2| \
        | s1 s2 s3 |   \ |s2 s3| , |s3 s1| , |s1 s2| /

S x R = - R x S

(a R) x S = R x (a S) = a (Rx S)

R x (S + T) = R x S + Rx T

R x R = 0

If a, b, c = angles between the unit vectors i, j,k and R Then the direction cosines are set by:

    cos a = (R . i) / |R|; cos b = (R . j) / |R|; cos c = (R . k) / |R|

|R x S| = Area of parrallagram with sides Rand S.

Component of R in the direction of S = |R|cos theta = (R . S) / |S|(scalar result)

Projection of R in the direction of S = |R|cos theta = (R . S) S/ |S| 2 (vector result)

Casa de Bender